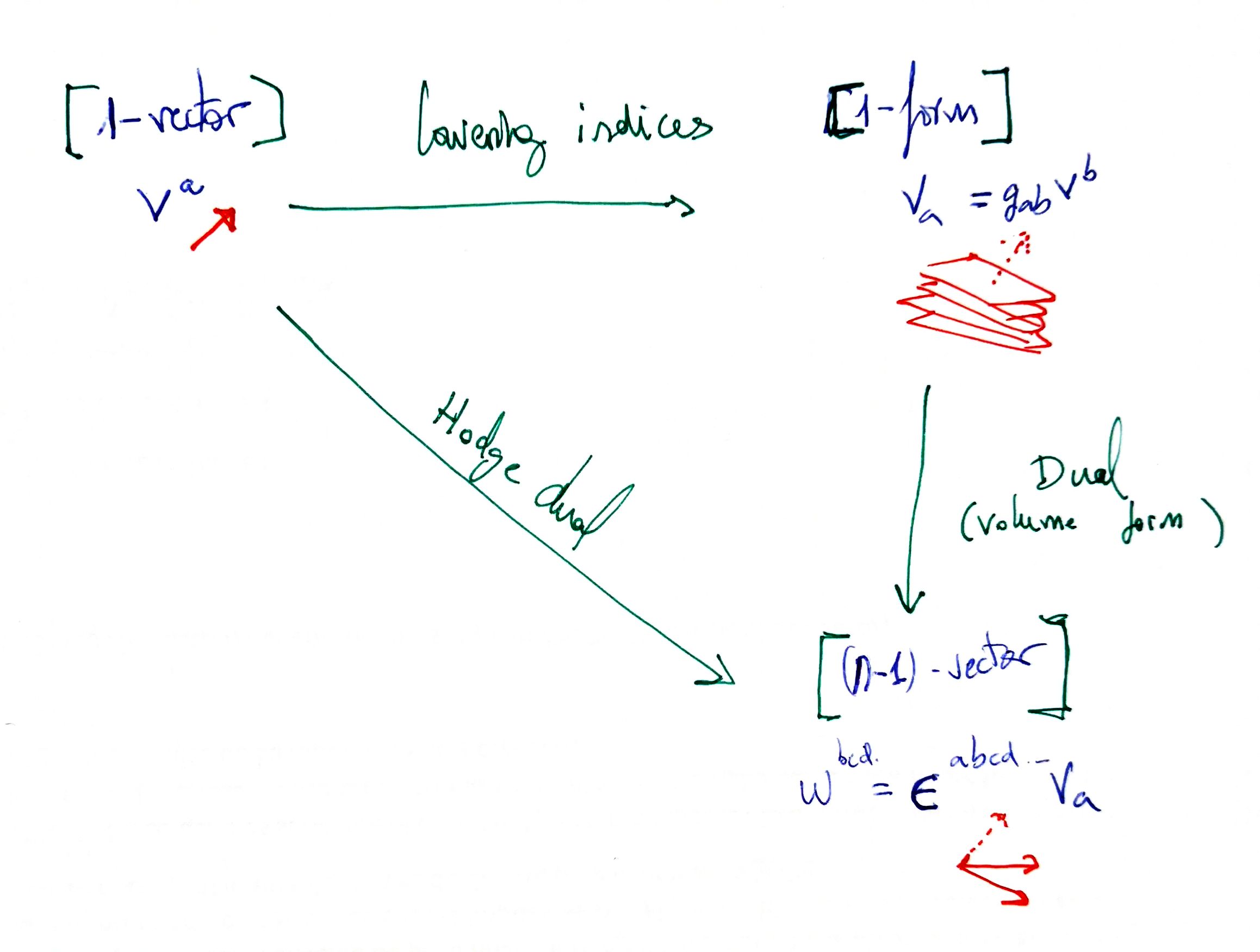
Hodge star

As explained in duality in exterior algebras, if we have a fixed volume form, for a simple $k$-vector $w$ we have the $(n-k)$-form

Reciprocally, to every $k$-form we can associate a $(n-k)$-vector at this way.

In the presence of a metric, we can take use this duality and then apply the raising and lowering indices. This is the Hodge star:

________________________________________

________________________________________

________________________________________

Author of the notes: Antonio J. Pan-Collantes

antonio.pan@uca.es